Summation Of Vectors Symbol

The kronecker delta symbol ij b.

Summation of vectors symbol. Scalar multiplication is represented in the same manners as algebraic multiplication. The levi civita totally antisymmetric tensor. Here we use an arrow to represent a vector. The triple vector product.

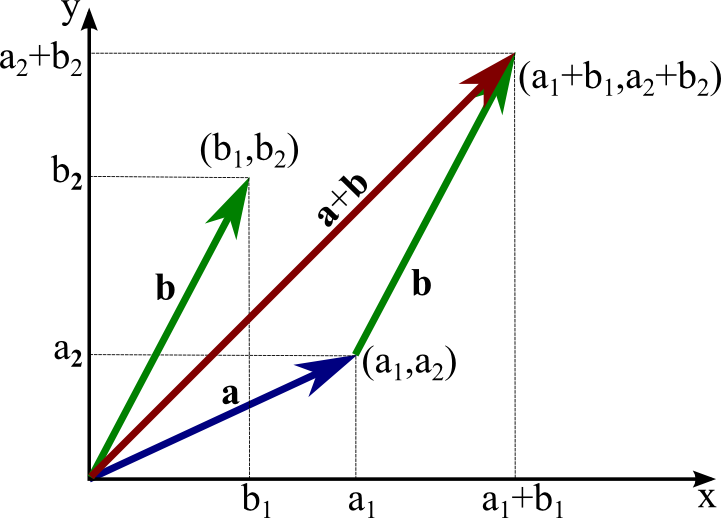
This index is referred to as a paired index. The term vector was introduced by william rowan hamilton as part of a quaternion which is a sum q s v of a real number s also called scalar and a 3 dimensional vector. The sum of two vectors u and v would be represented as. Its magnitude or length is written oq absolute value symbols.

Linear independence of. Note that the levi civita symbol can therefore be expressed as the determinant or mixed triple product of any of the unit vectors e 1 e 2 e 3 of a normalised and direct orthogonal frame of reference. Paired indices are summed. Linear equations and matrices.

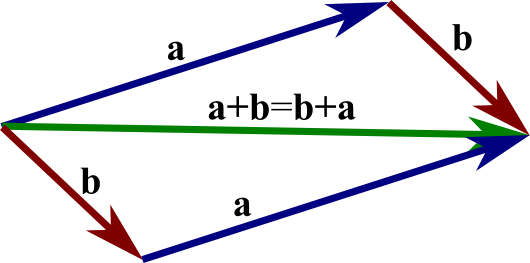
One of these is vector addition written symbolically as a b c vectors are conventionally written as boldface letters. The vector here can be written oq bold print or oq with an arrow above it. Note the compact notation where the summation over the spatial directions is dropped. In expressions involving vector or tensor indices whenever two indices are the same the same symbol it will be assumed that a sum over that index from 1 to 3 is to be carried out.

The einstein summation convention. Its length is its magnitude and its direction is indicated by the direction of the arrow. The einstein summation convention. It is this one that is in use.

A scalar beside a vector either or both of which may be in parentheses implies scalar multiplication. Geometrically the vector sum can be visualized by placing the tail of vector b at the head of vector a and drawing vector c starting from the tail of a and ending at the head of b so that it completes the triangle. Ijk det e i e j e k e i e j e. The triple scalar product.